Inspired by the 200th Anniversary of Ada Lovelace I thought it a good idea to implement the very first computer program (her Bernoulli calculator in Note G) in Javascript. Although I didn't use her method (I used the Akiyama-Tanigawa algorithm, instead) I did succeed in producing this rather nice piece:
I then wrote it in Ada. Because it seemed like the right thing to do.
I then wondered how many languages in which I'd professionally developed. And how many I knew, in total. It turns out the answer to the first question was a respectful 16, while the second was a none-to-shabby 26! So, I set about re-writing the same code in each of those languages. The purpose of the exercise was (and is) to learn, re-learn, and refresh my memory of these programming languages. Therefore, I'm more focused on the syntax, data types, and structure of the code. Less so on the dev environment, test suites, or accuracy of the algorithm.

Along with each code block, I have written some notes for building and running it, along with my own personal commentary. I picked the languages in an arbitrary order, so the concept of 'first' doesn't mean much. It is left as an exercise to the reader to determine the order I actually wrote them, based on my comments, and the evolution of the implementation.
Since some of those languages in which I've developed were assembly languages, and some were merely different dialects of BASIC, I haven't included them all here. (But I'll get to them all, eventually, I guess!) I've developed in several proprietary languages, too, which I doubt I'll ever be able to include.
I have presented this talk many times, here is but one recording: 
At the end of the list are my own thoughts on the learning on the process, as a whole. But in the mean time...
Procedure GCD[A,B] RESULT=A If B GCD[B,A mod B] RESULT=Param End If End Proc[RESULT] Procedure BERNOULLI[N] Dim NUMERATOR(N) Dim DENOMINATOR(N) Rem The for loop has inclusive limits For M=0 To N NUMERATOR(M)=1 DENOMINATOR(M)=1+M J=M While J>=1 NUMERATOR(J-1)=NUMERATOR(J-1)*DENOMINATOR(J) NUMERATOR(J-1)=NUMERATOR(J-1)-NUMERATOR(J)*DENOMINATOR(J-1) DENOMINATOR(J-1)=DENOMINATOR(J-1)*DENOMINATOR(J) NUMERATOR(J-1)=NUMERATOR(J-1)*J GCD[NUMERATOR(J-1),DENOMINATOR(J-1)] NUMERATOR(J-1)=NUMERATOR(J-1)/Param DENOMINATOR(J-1)=DENOMINATOR(J-1)/Param J=J-1 Wend Next M Rem I can't remember how to return two params, and don't want Rem to use globals, so I'm being bad and generating a string End Proc[Str$(NUMERATOR(0))+"/"+Str$(DENOMINATOR(0))] Print "Up to which bernoulli number shall I calculate?" Input HIGHEST For F=1 To HIGHEST BERNOULLI[F] Print Str$(F)+" : "+Param$ Next
package { import flash.display.Sprite; import flash.text.*; public class Bernoulli extends Sprite { public function Bernoulli() { for(var n:Number=1;n<17;++n) { var result:Array = calculateBernoulli(n); var myText:TextField = new TextField(); myText.text = result[0] + "/" + result[1]; myText.x = 10; myText.y = 10 + n*20; addChild(myText); } } protected function gcd(a:Number, b:Number) : Number { return b ? gcd(b, a%b) : a; } protected function reduce(numerator:Number, denominator:Number): Array{ var gcd: Number = gcd(numerator,denominator); return [numerator/gcd, denominator/gcd]; } protected function calculateBernoulli(n:Number) : Array { var numerator: Array = []; var denominator: Array= []; for(var m:Number=0;m<=n;++m) { numerator[m] = 1; denominator[m] = m+1; for(var j:Number=m;j>=1;--j) { // The calculation is: //A[j-1] = j * (A[j-1] - A[j]); // Change the fractions to have the same denom var newdenominator:Number = denominator[j-1] * denominator[j]; numerator[j-1] *= denominator[j]; numerator[j] *= denominator[j-1]; denominator[j-1] = denominator[j] = newdenominator; // Subtract numerator[j-1] = numerator[j-1] - numerator[j]; // Apply the j* .. bit numerator[j-1] *= j; // Reduce var r:Array = reduce(numerator[j-1], denominator[j-1]); numerator[j-1] = r[0]; denominator[j-1] = r[1]; } } return [ numerator[0] , denominator[0] ]; } } }
with Text_IO; use Text_IO; with Ada.Integer_Text_IO; use Ada.Integer_Text_IO; procedure bernoulli is Bern: Integer:= 4; begin Put_Line("Which B(n) would you like to compute:"); Get(Bern); declare N: array(1..Bern+1) of Integer; D: array(1..Bern+1) of Integer; new_denom: Integer; gcd_result: Integer; function GCD (X, Y: Integer) return Integer is X1: Integer:= X; Y1: Integer:= Y; Old_X : Integer; begin while (Y1 /= 0) loop -- x, y := y, x mod y Old_X := X1; X1 := Y1; Y1 := Old_X mod Y1; end loop; return X1; end GCD; begin for m in 1..Bern+1 loop N(m) := 1; D(m) := m; for j in reverse 2..m loop new_denom := D(j-1) * D(j); N(j-1) := N(j-1) * D(j); N(j) := N(j) * D(j-1); D(j-1) := new_denom; D(j) := new_denom; -- subtract N(j-1) := N(j-1) - N(j); -- Apply the j* .. bit N(j-1) := N(j-1) * (j-1); -- Reduce gcd_result := GCD(N(j-1), D(j-1)); N(j-1) := N(j-1)/gcd_result; D(j-1) := D(j-1)/gcd_result; end loop; end loop; Put(Integer'Image(N(1))); Put("/"); Put(Integer'Image(D(1))); end; end bernoulli;
After presenting my Javascript version on Facebook, my friend Bob suggested I should do it in Ada. It was the first language he was taught at University. So, over the course of a lunch hour, I learn just enough to write this code. I doubt it's idiomatic, but the development speed impressed me enough. (It's also why I haven't changed any of it - I want it left as a reminder of that day!)
#include <stdio.h> #include <malloc.h> int calcGCD(int a, int b) { return b ? calcGCD(b, a%b) : a; } struct Fraction { long numerator; long denominator; }; void calculateBernoulli(struct Fraction *pResult, const int n) { struct Fraction *pCalcList = (struct Fraction *)malloc(sizeof(struct Fraction) * (n+1)); long gcd; int m; int j; for(m=0;m<=n;++m) { pCalcList[m].numerator = 1; pCalcList[m].denominator = m+1; for(j=m;j>=1;--j) { pCalcList[j-1].numerator *= pCalcList[j].denominator; pCalcList[j-1].numerator -= pCalcList[j].numerator * pCalcList[j-1].denominator; pCalcList[j-1].denominator *= pCalcList[j].denominator; pCalcList[j-1].numerator *= j; gcd = calcGCD(pCalcList[j-1].numerator, pCalcList[j-1].denominator); pCalcList[j-1].numerator /= gcd; pCalcList[j-1].denominator /= gcd; } } pResult->numerator = pCalcList[0].numerator; pResult->denominator = pCalcList[0].denominator; free((void*)pCalcList); } void setup() { Serial.begin(9600); // open the serial port at 9600 bps: struct Fraction result; int n; for(n=1;n<19;++n) { calculateBernoulli(&result, n); Serial.print(n); Serial.print(" : "); Serial.print(result.numerator); Serial.print("/"); Serial.println(result.denominator); } } void loop() { }
This is a copy of the C version, where the output method was changed to use Serial.print and main() was replaced by the setup-loop pair of functions. I included it only for completeness. (It's not to increase my language count, so I don't expect extra credit for doing so ;)
#!/bin/bash function gcd() { # We can't return negative values so abs() them if [ $1 -lt 0 -a $2 -lt 0 ]; then gcd $(expr 0 - $1) $(expr 0 - $2) return $? fi if [ $1 -lt 0 ]; then gcd $(expr 0 - $1) $2 return $? fi if [ $2 -lt 0 ]; then gcd $1 $(expr 0 - $2) return $? fi # Usual recursion appears here if [ $2 -eq 0 ]; then return $1 fi gcd $2 $(($1 % $2)) } function bernoulli { declare -a num declare -a den local GCD for M in `seq 0 $1`; do num[$M]=1 den[$M]=$(($M + 1)) for J in `seq $M -1 1`; # from inc last do JM1=$(($J - 1)) # n[j-1] *= d[j] num[$JM1]=$(expr ${num[$JM1]} \* ${den[$J]}) # n[j-1] -= n[j]*d[j-1] TEMPCALC=$(expr ${num[$J]} \* ${den[$JM1]}) num[$JM1]=$(expr ${num[$JM1]} - $TEMPCALC) # d[j-1] *= d[j] den[$JM1]=$(expr ${den[$JM1]} \* ${den[$J]}) # n[j-1] *= j num[$JM1]=$(expr ${num[$JM1]} \* $J) # Simplify gcd ${num[$JM1]} ${den[$JM1]} GCD=$? if [ $GCD -ne 0 ]; then num[$JM1]=$(expr ${num[$JM1]} / $GCD) den[$JM1]=$(expr ${den[$JM1]} / $GCD) fi done done echo ${num[0]} \/ ${den[0]} } # Beyond 9 and expr exceeds its numerical range # (and as soon as errors return, the code breaks) for N in `seq 1 9`; do RESULT=$(bernoulli $N) echo $N ":" $RESULT done
#!/bin/bash function gcd() { if [ $2 -eq 0 ]; then echo $1 else gcd $2 $(($1 % $2)) fi } function bernoulli { declare -a num declare -a den local GCD for M in `seq 0 $1`; do num[$M]=1 den[$M]=$(($M + 1)) for J in `seq $M -1 1`; # from inc last do JM1=$(($J - 1)) # n[j-1] *= d[j] num[$JM1]=$(expr ${num[$JM1]} \* ${den[$J]}) # n[j-1] -= n[j]*d[j-1] TEMPCALC=$(expr ${num[$J]} \* ${den[$JM1]}) num[$JM1]=$(expr ${num[$JM1]} - $TEMPCALC) # d[j-1] *= d[j] den[$JM1]=$(expr ${den[$JM1]} \* ${den[$J]}) # n[j-1] *= j num[$JM1]=$(expr ${num[$JM1]} \* $J) # Simplify GCD=$(gcd ${num[$JM1]} ${den[$JM1]}) if [ $GCD -ne 0 ]; then num[$JM1]=$(expr ${num[$JM1]} / $GCD) den[$JM1]=$(expr ${den[$JM1]} / $GCD) fi done done echo ${num[0]} \/ ${den[0]} } for N in `seq 1 19`; do RESULT=$(bernoulli $N) echo $N ":" $RESULT done
Bash is not the answer whenever the question "in what language shall I perform number crunching" but, with expr and seq it functions adaquately for small tasks, if slow. The syntax for both the maths operations and arrays, however, are ugly and (apparently) inconsisent if you're not au fait will the minutiae of bash. So much so that I used temporary values.
COMMENT Bernoulli calculator. A version of the very first computer program ever written... define gcd set gcdResult to 0 while gcdB <> 0 set swap to gcdB set gcdB to gcdA % gcdB set gcdA to swap set gcdResult to gcdA end if end define define reduce set gcdA = nj1 set gcdB = dj1 call gcd if gcdResult <> 0 set nj1 to nj1 / gcdResult set dj1 to dj1 / gcdResult end if end define define calculate array numerator create size bernoulli+1 array denominator create size bernoulli+1 COMMENT When bernoulli is set to '2', this loops with m=1, m=2, and m=3 COMMENT So we need to think of 1-indexed arrays, not 0-based. (Like Ada.) repeat bernoulli+1 as m array numerator set index m to 1 array denominator set index m to m+1 if m > 1 repeat m-1 as jloop COMMENT Since Bolt loops (currently) only count up, we use this variable to reverse the order set j as m-jloop + 1 COMMENT Copy the array elements into variables, so they can be operated on array numerator get index j into nj array denominator get index j into dj array numerator get index j-1 into nj1 array denominator get index j-1 into dj1 COMMENT Now perform the calculation set nj1 to nj1 * dj set nj1 to nj1 - (nj * dj1) set dj1 to dj1 * dj set nj1 to nj1 * (j-1) COMMENT Reduce the fraction to its smallest form CALL reduce COMMENT copy the results back array numerator set index j-1 to nj1 array denominator set index j-1 to dj1 end repeat end if end repeat COMMENT Move the result into gcdN and gcdD so the calling code can use it array numerator get index 1 into gcdN array denominator get index 1 into gcdD end define define print_fraction if gcdN = 0 print at 150 bernoulli*20 + 20 bernoulli " : " 0 else print at 150 bernoulli*20 + 20 bernoulli " : " gcdN "/" gcdD end if end define COMMENT Our calculation code starts here... color text "red" print at 10 25 "Working..." color text "black" repeat 16 as bernoulliloop set bernoulli to bernoulliloop-1 call calculate call print_fraction end repeat color text "red" print at 430 320 "Complete!"
This version shows off the power of the Bolt language... as well as it's limitations. Notably that, being a teaching language, it enforces good technique over speed of development which actually means it slows down development for an experience developer. Specifically, these areas are:
* not dividing by zero (even when 0/0 is definied as 0 in most languages)
* simplifying loops and arrays by starting them from one, not zero
* all repeat loops iterate from 1 to N, without the option of working backwards from N to 1
* requiring that all array elements are copied to local variables so that calculations can be performed, before copying them back (this stops obtuse mathematics from appearing that can scare the youngsters)
This means we end up having a loop counter (bernoulliloop or jloop), for example, and a 'set' instruction immediately afterwards to 'fix' it.
There are also a few adopted conventions so that we can write the whole algorithm without local variables, or recursion. But overall, it's a decent (if long-winded) implementation of the algorithm. (And pretty fast, considering it's interpreted in Javasacript!)
Sub Main() For n = 1 TO 17 r = calculateBernoulli(n) displayFraction(r) End For End Sub Function displayFraction(fraction as Object) as Void divisor_sign = "/" r = StrI(fraction.n) + divisor_sign + StrI(fraction.d) print r End Function Function calculateBernoulli(n as Integer) as Object array = CreateObject("roArray", n+1, true) For m=0 TO n array[m] = { n: 1, d: m+1 } For j=m TO 1 Step -1 new_denom = array[j-1].d * array[j].d array[j-1].n = array[j-1].n * array[j].d array[j].n = array[j].n * array[j-1].d array[j-1].d = new_denom array[j].d = new_denom array[j-1].n = j * (array[j-1].n - array[j].n) reduceFraction(array[j]) reduceFraction(array[j-1]) End For End For return array[0] End Function Function calculateGCD(a as Integer, b as Integer) as Integer If b return calculateGCD(b, a MOD b) Else return a End If End Function Function reduceFraction(fraction as Object) as Void gcd = calculateGCD(fraction.n, fraction.d) fraction.n = fraction.n / gcd fraction.d = fraction.d / gcd End Function
The port to this language was straightforward, with only the += and *= operators needing the more explicit x = x * ... version. I also needed to reduce both fractions in order to get any kind of precision with 4 byte integers. Even then, I only managed 12 results, before the number system broke down.
My primary reason for writing this version is that I'd recently started working for the company that created the language (BrightSign) and thought it prudent to learn a little of it. Naturally, this was an easy example with which to kick its tyres.
#include <stdio.h> #include <malloc.h> int calcGCD(int a, int b) { return b ? calcGCD(b, a%b) : a; } struct Fraction { long numerator; long denominator; }; void calculateBernoulli(struct Fraction *pResult, const int n) { struct Fraction *pCalcList = (struct Fraction *)malloc(sizeof(struct Fraction) * (n+1)); long gcd; int m; int j; for(m=0;m<=n;++m) { pCalcList[m].numerator = 1; pCalcList[m].denominator = m+1; for(j=m;j>=1;--j) { pCalcList[j-1].numerator *= pCalcList[j].denominator; pCalcList[j-1].numerator -= pCalcList[j].numerator * pCalcList[j-1].denominator; pCalcList[j-1].denominator *= pCalcList[j].denominator; pCalcList[j-1].numerator *= j; gcd = calcGCD(pCalcList[j-1].numerator, pCalcList[j-1].denominator); pCalcList[j-1].numerator /= gcd; pCalcList[j-1].denominator /= gcd; } } pResult->numerator = pCalcList[0].numerator; pResult->denominator = pCalcList[0].denominator; free((void*)pCalcList); } int main(const int argc, const char *argv[]) { struct Fraction result; int n; for(n=1;n<19;++n) { calculateBernoulli(&result, n); printf("%d : %ld/%ld\n", n, result.numerator, result.denominator); } return 0; }
It's shocking that I had forgotten so much about writting _basic_ C! That is, without all the modern extensions.
The use of malloc and free. The use of struct. (I was tempted to typedef a few things, but decided to leave it pure as an aide memoire for language historians.) Passing pointers, instead of references. printf.
At least I remembered to clean up my malloc's, and not pass pCalcList[0] back.
window.bernoulli ?= {} window.bernoulli.calculate = (n) -> calculate(n) # No ternary gcd = (a,b) -> if b gcd(b, a%b) else a reduce = (f) -> # Don't use gcd var here, because it's trashed by the method name result = gcd(f.n, f.d) n: f.n/result d: f.d/result calculate = (n) -> fraction = [] for m in [0..n] fraction[m] = n: 1 d: m+1 for j in [m..1] by -1 # f[j-1] = j * f[j-1]-f[j] nd = fraction[j-1].d * fraction[j].d fraction[j-1].n *= fraction[j].d fraction[j].n *= fraction[j-1].d fraction[j-1].d = fraction[j].d = nd fraction[j-1].n -= fraction[j].n fraction[j-1].n *= j fraction[j-1] = reduce(fraction[j-1]) fraction[0]
<div id="output"></div> <script type="text/javascript"> var b; for(var n=0;n<20;++n) { b = bernoulli.calculate(n); $('#output').append(b.n + "/" + b.d + "<br>"); } </script>
I don't really like Coffeescript, because it always feels like it was developed to safe the "effort" of learning the good parts of Javascript, but I see nothing wrong in it as a language, per se.
It has the same problems of looping backwards as many languages, and has different scoping rules that mean a local variable with a name matching a global function will cause problems. (See gcd for this.) Since the language understood (and took efforts to improve) scoping, it seems strange that they solved one problem, but created another.
#include <iostream> #include <vector> int calcGCD(int a, int b) { return b ? calcGCD(b, a%b) : a; } class Fraction { public: Fraction() { numerator = denominator = 1; } void reduce(){ int gcd = calcGCD(numerator, denominator); numerator /= gcd; denominator /= gcd; } void assign(int n, int d) { numerator = n; denominator = d; } Fraction& operator-=(const Fraction& fraction) { Fraction rhs(fraction); numerator *= rhs.denominator; rhs.numerator *= denominator; denominator *= rhs.denominator; rhs.denominator = denominator; numerator -= rhs.numerator; reduce(); return *this; } Fraction& operator*=(const int multiplier) { numerator *= multiplier; reduce(); return *this; } friend std::ostream& operator<<(std::ostream& os, const Fraction& fraction) { fraction.numerator ? os << fraction.numerator << '/' << fraction.denominator : os << 0; return os; } private: int numerator; int denominator; }; Fraction calculateBernoulli(const int n) { std::vector<Fraction> calcList; calcList.resize(n+1); for(int m=0;m<=n;++m) { calcList[m].assign(1, m+1); for(int j=m;j>=1;--j) { calcList[j-1] -= calcList[j]; calcList[j-1] *= j; } } return calcList[0]; } int main(const int argc, const char *argv[]) { for(int n=1;n<15;++n) { std::cout << calculateBernoulli(n) << '\n'; } return 0; }
As a long time developer in C++ (I started in 1994) I had to roll-my-own Fraction class for this. I also forced myself into using streams, even though I rarely used them since my C++ work was always in embedded systems and graphics and so I had a custom library for rendering output.
# Compute the Bernoulli numbers, the worlds first computer program # Taken from the 'Ada 99' project, https://marquisdegeek.com/code_ada99 class Fraction def initialize(n : Int64, d : Int64) @numerator = n @denominator = d end def numerator @numerator end def denominator @denominator end def subtract(rhs_fraction) rhs_numerator = rhs_fraction.numerator * @denominator rhs_denominator = rhs_fraction.denominator * @denominator @numerator *= rhs_fraction.denominator @denominator *= rhs_fraction.denominator @numerator -= rhs_numerator self.reduce end def multiply(value) @numerator *= value end def reduce gcd = gcd(@numerator, @denominator) @numerator /= gcd @denominator /= gcd end def to_s @numerator == 0 ? 0 : @numerator.to_s + '/' + @denominator.to_s end end def gcd(a, b) # we need b>0 because b on its own isn't considered true b > 0 ? gcd(b, a % b) : a end def calculate_bernoulli(bern) row = [] of Fraction 0_i64.step(bern) do |m| row << Fraction.new(1_i64, m + 1) m.step(1, -1) do |j| row[j - 1].subtract(row[j]) row[j - 1].multiply(j) row[j - 1].reduce end end row[0] end 1_i64.step(30_i64) do |bern| puts calculate_bernoulli(bern).to_s end
A few gotchas in here, such as the b>0 truthiness and the surprisingly low limit of Int32. (I later upgraded the code to use 64 bit integers.) But otherwise, fairly straight forward. Being such a new language, I don't know any (personally) to ask to help or advise. Details on https://crystal-lang.org Online version at https://play.crystal-lang.org/#/r/1eao
: gcd ( in: a b out: gcd ) dup 0= if drop ( result is the a remaining on top ) else dup ( a b -- a b b ) rot ( a b b -- b a b ) rot ( b a b -- b b a ) mod ( b b a -- b b%a ) recurse ( some implementations, like the Jupiter Ace, let you use gcd here ) then ; : fr_reduce ( in: n d out: n' d' ) over ( only reduce fraction if n!=0 as 0/0 fails on gforth ) 0<> if over ( n d n ) over ( n d n d ) gcd ( n d gcd ) swap ( n gcd d) over ( n gcd d gcd ) / ( n gcd d' ) rot ( gcd d' n ) rot ( d' n gcd ) / ( d' n' ) swap ( n' d' ) then ; : fr_print ( in: n d out: -- ) swap ( n d -- d n ) ?dup 0= ( handle the case of 0/d ) if drop 0 . else ( d n ) . 47 emit ( / ) . then ; : calculate { num denom } 1 + 0 ( -- N+1 0, limit and start for 'm' loop) do 1 num I cells + ! ( write 1 to numerator ) I 1 + denom I cells + ! ( write 1+i to denominator ) I ( j=m : loop counter on top of stack ) begin ( loop while j>=1 ) -1 + dup 0 >= ( test is with 0 since we're using a post-decrement ) while ( top of stack is j-1, not j ) ( create a do-loop which executes once, so I can use 'I' instead of duplicating the stack top ) ( also patch it so that I is _actually_ j and not j-1 ) dup 1 + dup 1 + swap do ( rowNum[j - 1] *= rowDen[j]; ) num I 1 - cells + @ ( =rowNum[j - 1] ) denom I cells + @ ( =rowDen[j ] ) * num I 1 - cells + ! ( rowNum[j - 1] = ) ( rowNum[j - 1] -= rowNum[j] * rowDen[j - 1]; ) num I 1 - cells + @ ( =rowNum[j - 1] ) num I cells + @ ( =rowNum[j] ) denom I 1 - cells + @ ( =rowDen[j - 1] ) * ( rhs ) - num I 1 - cells + ! ( rowNum[j - 1]= ) ( rowDen[j - 1] *= rowDen[j]; ) denom I 1 - cells + @ ( rowDen[j - 1] ) denom I cells + @ ( rowDen[j] ) * denom I 1 - cells + ! ( rowDen[j - 1] ) ( c[j-1] *= j ) num I 1 - cells + @ ( rowNum[j - 1] ) I * dup ( duped so we can use fr_reduce afterwards ) num I 1 - cells + ! ( but store it back in rowNum[j - 1] for the next iteration ) ( reduce it ) denom I 1 - cells + @ fr_reduce denom I 1 - cells + ! num I 1 - cells + ! loop repeat drop ( remove the loop counter ) loop num @ denom @ ; : bernoulli { num denom } 30 0 do I . ." : " I num denom calculate fr_print cr loop ;
This was my biggest disappointment, to date, as the result I achieved was significantly less elegant than I'd hope for. More so since I'd had a great start to the build, working on the gcd and reduce methods on a Jupiter Ace emulator on Christmas Eve!
To start, I spent/wasted so many hours looking for a way of creating arrays within a compiled word to give me some workspace memory :( I'm sure it's possible, but I couldn't see any way of making it work, outside of immediate mode. Therefore, I create the arrays in immediate mode (using the -e param in gforth) and pass their addresses into the bernoulli word. (This leads to potential problems with mismatched sizes of arrays, and calculation.)
Also, I tried to work out a method whereby all calculations were performed on the stack. I gave up sooner than I should have. Again, because getting the address of the storage (and holding it a convenient variable) was problematic. I'm sure there's a way of doing this.
On the plus side, the result is brilliantly fast, and the cells allow for quite high precision - so much so, that I don't mind showing off the first 30 results.
I also impressed myself by inventing (re-inventing?) the 'dup 1 + dup 1 + swap' trick, which allowed me to create a do-loop that executes only once, so I can use 'I' instead of duplicating the stack top as the loop iterator.
module bernoulli implicit none type fraction integer:: num, denom end type contains recursive function calc_gcd(a, b) result(gcd) integer, intent(in):: a,b integer:: gcd if (b == 0) then gcd = a else gcd = calc_gcd(b, MOD(a,b)) end if end function calc_gcd function calculate( n ) result(result) integer:: n type(fraction):: result type(fraction), dimension(:), allocatable:: a integer:: gcd integer:: m, j allocate(a(0:n)) do m = 0, n a(m)%num = 1 a(m)%denom = m+1 do j = m, 1, -1 a(j-1)%num = a(j-1)%num * a(j)%denom a(j-1)%num = a(j-1)%num - (a(j)%num * a(j-1)%denom) a(j-1)%denom = a(j-1)%denom * a(j)%denom a(j-1)%num = a(j-1)%num * j gcd = calc_gcd(a(j-1)%num, a(j-1)%denom) a(j-1)%num = a(j-1)%num / gcd a(j-1)%denom = a(j-1)%denom / gcd end do end do result%num = a(0)%num result%denom = a(0)%denom end function calculate end module program main use bernoulli integer:: i type(fraction):: answer do i = 1,20 answer = calculate(i) if (answer%num == 0) then print *, i, " : ", 0 else print *, i, " : ", answer%num, "/", answer%denom end if end do end program
I was quite happy that I managed to utilize types and recursive functions with the intent keyword. I wasn't so happy in wasting so long in not understanding the array shape. In Fortran arrays start from 0... but only if you ask it! Consequently, my allocate(a(n)) needed to be changed to allocate(a(0:n)). Missing this minor point caused me to experiment with two arrays (numerator & denominator) since I was getting crashes. Stupid!
package main import "fmt" const message string = "Calculating Bernoulli numbers..." type Fraction struct { numerator int denominator int } func (f Fraction) String() string { if f.numerator == 0 { return "0"; } sign := []string{"", "-", ""} which_sign := 0 n := f.numerator d := f.denominator if n < 0 { n = -n which_sign++ } if d < 0 { d = -d which_sign++ } return fmt.Sprintf("%s%d/%d", sign[which_sign], n, d) } func gcd(a int, b int) int { if b == 0 { return a; } return gcd(b, a%b) } func simplify(a int, b int) (int, int) { gcd := gcd(a, b) return a/gcd, b/gcd } func calculateBernoulli(n int) Fraction { rowNum := make([]int, n+1) rowDen := make([]int, n+1) for m := range rowNum { rowNum[m] = 1 rowDen[m] = m+1 for j:=m; j>0; j-- { //A[j-1] = j * (A[j-1] - A[j]); // Ensure denominators are equal newDen := rowDen[j - 1] * rowDen[j] rowNum[j - 1] *= rowDen[j] rowNum[j] *= rowDen[j - 1] rowDen[j] = newDen rowDen[j - 1] = newDen // Subtract rowNum[j - 1] -= rowNum[j] // Multiply rowNum[j - 1] *= j // Reduce rowNum[j - 1], rowDen[j - 1] = simplify(rowNum[j - 1], rowDen[j - 1]) } } return Fraction{numerator: rowNum[0], denominator: rowDen[0]} } func main() { fmt.Println(message) for bern:= 0; bern<17; bern++ { fmt.Println(calculateBernoulli(bern)) } }
package main import "fmt" const message string = "Calculating Bernoulli numbers..." type Fraction struct { numerator int denominator int } func (f Fraction) String() string { if f.numerator == 0 { return "0"; } sign := []string{"", "-", ""} which_sign := 0 n := f.numerator d := f.denominator if n < 0 { n = -n which_sign++ } if d < 0 { d = -d which_sign++ } return fmt.Sprintf("%s%d/%d", sign[which_sign], n, d) } func gcd(a int, b int) int { if b == 0 { return a; } return gcd(b, a%b) } func simplify(a int, b int) (int, int) { gcd := gcd(a, b) return a/gcd, b/gcd } func calculateBernoulli(n int) Fraction { rowNum := make([]int, n+1) rowDen := make([]int, n+1) for m:= range rowNum { rowNum[m] = 1 rowDen[m] = m+1 for j:=m; j>0; j-- { //A[j-1] = j * (A[j-1] - A[j]); rowNum[j - 1] *= rowDen[j]; rowNum[j - 1] -= rowNum[j] * rowDen[j - 1]; rowDen[j - 1] *= rowDen[j]; // Multiply rowNum[j - 1] *= j // Reduce rowNum[j - 1], rowDen[j - 1] = simplify(rowNum[j - 1], rowDen[j - 1]) } } return Fraction{numerator: rowNum[0], denominator: rowDen[0]} } func main() { fmt.Println(message) for bern:= 0; bern<17; bern++ { fmt.Println(calculateBernoulli(bern)) } }
Here I'm mixing the data types: Fraction in some places, and numer/denom integer pairs in others. This is intentional, since I wanted Golang's ability to return multiple values.
I also liked the method to determine the sign of the fraction, even though its full functionality won't get used in this case. (The case of -/- can't happen, AFAIK.)
I was (and am still) very disappointed by the ability for Go to maintain accuracy when the numbers get large. It was tempting to move it to bigints, but it was late, so I postponed it.
import java.lang.System; import java.lang.Math; public class Bernoulli { private class BernoulliFraction { private int numerator; private int denominator; public BernoulliFraction(int n, int d) { numerator = n; denominator = d; } public int gcd(int n, int d) { return d!=0 ? gcd(d, n%d) : n; } public void simplify() { int gcd = gcd(numerator, denominator); numerator /= gcd; denominator /= gcd; } public void sub(BernoulliFraction rhs) { numerator *= rhs.denominator; numerator -= rhs.numerator * denominator; denominator *= rhs.denominator; simplify(); } public void mul(int rhs) { numerator *= rhs; simplify(); } public String toString() { if (numerator == 0) { return "0"; } else if (denominator == 1) { return Integer.toString(numerator); } String sign = Math.signum(numerator) == Math.signum(denominator) ? "" : "-"; return sign + Integer.toString(Math.abs(numerator)) + "/" + Integer.toString(Math.abs(denominator)); } } public BernoulliFraction calculate(int n) { BernoulliFraction[] bernoulli = new BernoulliFraction[n+1]; for(int m=0; m<=n; ++m) { bernoulli[m] = new BernoulliFraction(1, m+1); for(int j=m; j>=1; --j) { bernoulli[j-1].sub(bernoulli[j]); bernoulli[j-1].mul(j); } } return bernoulli[0]; } public static void main(String[] args) { Bernoulli bernoulli = new Bernoulli(); int n = Integer.parseInt(args[0]); for (int i=0; i<n; ++i) { System.out.println(bernoulli.calculate(i).toString()); } } }
Getting the development environment work was the biggest pain, here, as the Linux version of the compiler and run-time (for some reason) decided to not match :( And the use of the -target 1.4 option of javac wasn't helping. So I (reluctantly) re-installed Eclipse for the first time in 5 years. On the plus side, my machine is now fast enough to run it!
I also decided to use the 3-line version of the subtract method, which doesn't affect A[j], to gain precision.
function reduce(numerator,denominator){ var gcdfn = function gcd(a,b){ return b ? gcdfn(b, a%b) : a; }; gcd = gcdfn(numerator,denominator); return [numerator/gcd, denominator/gcd]; } function calculateBernoulli(n) { var numerator = []; var denominator = []; for(var m=0;m<=n;++m) { numerator[m] = 1; denominator[m] = (m+1); for(var j=m;j>=1;--j) { // The calculation is: //A[j-1] = j * (A[j-1] - A[j]); // Change the fractions to have the same denom var newdenominator = denominator[j-1] * denominator[j]; numerator[j-1] *= denominator[j]; numerator[j] *= denominator[j-1]; denominator[j-1] = denominator[j] = newdenominator; // Subtract numerator[j-1] = numerator[j-1] - numerator[j]; // Apply the j* .. bit numerator[j-1] *= j; // Reduce var r = reduce(numerator[j-1], denominator[j-1]); numerator[j-1] = r[0]; denominator[j-1] = r[1]; } } return [ numerator[0] , denominator[0] ]; }
function calculateBern(n) { function g(a,b){ return b ? g(b, a%b) : a; } var N = []; var D = []; var m=0, j, gcd; var jm1; var tempNjm1, tempDjm1; for(;m<=n;) { N[j=jm1=m] = 1; D[m] = ++m; for(;jm1;) { tempNjm1 = N[--jm1] * D[j] - (N[j] *= tempDjm1 = D[jm1]); // Reduce r = g(tempNjm1*=j, tempDjm1 = D[j] = tempDjm1 * D[j]); N[jm1] = tempNjm1/r; D[--j] = tempDjm1/r; } } return [ N[0] , D[0] ]; }
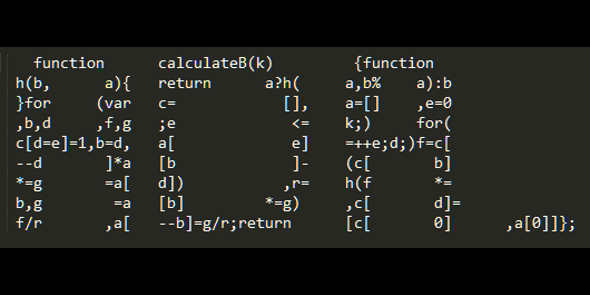
function calculateB(k){function h(b,a){return a?h(a,b%a):b}for(var c=[],a=[],e=0,b,d,f,g;e<=k;)for(c[b=d=e]=1,a[e]=++e;d;)f=c[--d]*a[b]-(c[b]*=g=a[d]),r=h(f*=b,g=a[b]*=g),c[d]=f/r,a[--b]=g/r;return [c[0],a[0]]};
<div id="output"></div> <script type="text/javascript" src="basic.js"></script> <script type="text/javascript"> var b; for(var n=0;n<20;++n) { b = calculateBernoulli(n); document.getElementById("output").innerHTML = document.getElementById("output").innerHTML + b[0] + "/" + b[1] + "<br>" } </script>
The first one I wrote, since I was doing a lot of Javascript work at the time. The idea to optimize the algorithm into the smallest possible space happened one Saturday morning because I was curious to see if I could get the code into 140 characters to share in a tweet. I spent about 3 hours trying. Ultimately, I couldn't, and had to resort to the image.
The ASCII art image was hand generated. The size of the letters was determined by the keywords which _couldn't_ be positioning anywhere else. e.g. function and return.
(defun gcd2 (a b) (if (= b 0) a (gcd2 b (mod a b))) ) (defstruct fraction numerator denominator ) (defun fraction-print (f) (if (= (fraction-numerator f) 0) (write 0) (write (list (fraction-numerator f) '/ (fraction-denominator f)))) ) (defun fraction-subtract (f1 f2) (setf (fraction-numerator f1) (* (fraction-numerator f1) (fraction-denominator f2) ) ) (setf (fraction-numerator f1) (- (fraction-numerator f1) (* (fraction-numerator f2) (fraction-denominator f1)) ) ) (setf (fraction-denominator f1) (* (fraction-denominator f1) (fraction-denominator f2) ) ) (return-from fraction-subtract f1) ) (defun fraction-multiply (f value) (setf (fraction-numerator f) (* (fraction-numerator f) value) ) (return-from fraction-multiply f) ) (defun fraction-reduce (f) (setq gcd (gcd2 (fraction-numerator f) (fraction-denominator f))) (setf (fraction-numerator f) (/ (fraction-numerator f) gcd) ) (setf (fraction-denominator f) (/ (fraction-denominator f) gcd) ) (return-from fraction-reduce f) ) (defun calculate-bernoulli (bern) (setf row (make-array (+ 1 bern))) (setq m 0) ; from 0 to bern (loop ; row (setf (aref row m) (make-fraction :numerator 1 :denominator (+ m 1) )) (loop for j from m downto 1 do (list ; In other languages the first parameter would be considered a reference ; as we directly change the value of row[j-1] (fraction-reduce (fraction-multiply (fraction-subtract (aref row (- j 1)) (aref row j)) j) ) )) (setq m (+ m 1)) (when (> m bern) (return m)) ) (return-from calculate-bernoulli (aref row 0)) ) (loop for bern from 1 to 20 do (list (write bern) (princ " : ") (fraction-print (calculate-bernoulli bern)) (terpri) ))
Whoah! One of the holy grails, and I finally managed it. It's not pretty, and it's certainly not idiomatic, but I now know why people love and hate LISP, according to temprament.
Perhaps strangely, the reverse order (i.e. stack based) handling gave me the least amount of trouble. (No doubt to my love and minor experience with Forth.) What did, however, was getting a loop to count down and terminate correctly! I had to switch my approach from setq-loop to loop-for. This stopped the first iteration from being evaluated.
An online version is available from https://goo.gl/JaZJji
function gcd(a, b) if b == 0 then return a else return gcd(b, math.mod(a, b)) end end function simplify(a, b) local gcd = gcd(a, b) return a/gcd, b/gcd end function calculate(bernoulli) local n = {} local d = {} for m=0,bernoulli do n[m] = 1 d[m] = m + 1 for j=m,1,-1 do n[j-1] = n[j-1] * d[j] n[j-1] = n[j-1] - (n[j] * d[j-1]) d[j-1] = d[j-1] * d[j] n[j-1] = n[j-1] * j -- If we don't keep simplifying the numbers, lua runs -- out of capacity to computer them! n[j-1], d[j-1] = simplify(n[j-1], d[j-1]) end end return simplify(n[0], d[0]) end -- main starts here io.write("Up to which Bernoulli number would you like to compute?") local count = io.read() local n,d for i=0,count do io.write(i, " : ") n,d = calculate(i) io.write(n, "/", d, "\n") end
A simple conversion this one. By the time I got to this one, I'd given up on the 'full' version of the subtraction, and just used the 3 line code which doesn't affect the a[j] element. Even so, I was surprised by the need to simplify at each step. Without it, the numbers break down _very_ quickly!
(* Taken from the 'Ada 99' project, https://marquisdegeek.com/code_ada99 *) program BernoulliForAda99; type Fraction = object private numerator, denominator: Int64; public procedure assign(n, d: Int64); procedure subtract(rhs: Fraction); procedure multiply(value: Int64); procedure reduce(); procedure writeOutput(); end; function gcd(a, b: Int64):Int64; begin if (b = 0) then gcd := a else gcd := gcd(b, a mod b) end; procedure Fraction.writeOutput(); begin write(numerator); if (numerator <> 0) then begin write('/'); write(denominator); end; end; procedure Fraction.assign(n, d: Int64); begin numerator := n; denominator := d; end; procedure Fraction.subtract(rhs: Fraction); begin numerator := numerator * rhs.denominator; numerator := numerator - (rhs.numerator * denominator); denominator := denominator * rhs.denominator; end; procedure Fraction.multiply(value: Int64); begin numerator := numerator * value; end; procedure Fraction.reduce(); var gcdResult: Int64; begin gcdResult := gcd(numerator, denominator); begin numerator := numerator div gcdResult; (* div is Int64 division *) denominator := denominator div gcdResult; (* could also use round(d/r) *) end; end; function calculateBernoulli(n: Int64) : Fraction; var m, j: Int64; results: array of Fraction; begin setlength(results, n); for m:= 0 to n do begin results[m].assign(1, m+1); for j:= m downto 1 do begin results[j-1].subtract(results[j]); results[j-1].multiply(j); results[j-1].reduce(); end; end; calculateBernoulli := results[0]; end; (* Main program starts here *) var b: Int64; result: Fraction; begin writeln('Calculating Bernoulli numbers...'); for b:= 1 to 25 do begin write(b); write(' : '); result := calculateBernoulli(b); result.writeOutput(); writeln; end; end.
Oh! Pascal! How I've missed you... NOT! I remember the "declare before use" rule, and that for loops need downto for decrementing steps, but managed to forget almost all of the other gotchas. For example, div is for integer division (not / which is for Doubles.) Also, there's a separate keyword for functions (which return a value) and procedures (which do not.) Oh, there's so many semicolons that I ended putting them in too many places and short-circuited a for block. (It took 15 minutes or more to find that bug, with writeln, all of things.)
As for the Bernoulli algorithm itself, it wasn't a difficult port per se. I switch to Int64 upon realized the limit of integers. Otherwise, it was strange going back to a language with such distinct definition and declaration sections but, given the age and the "declare before use" rules, it's a necessary evil. And no worse than C.
Oh, and the bounds of the for loops are inclusive.
#!/usr/bin/perl use strict; use warnings; use Math::Fraction; sub calculate { my ($n) = @_; my @a = (); for my $m (0..$n) { $a[$m] = frac(1, $m+1); foreach my $j (reverse 1..$m) { $a[$j-1] = $a[$j-1]- $a[$j]; $a[$j-1] *= $j; } } $a[0]->reduce } for my $bern (0..17) { my $result = calculate($bern); print $result . "\n"; }
I'd forgotten how much I hated getting CPAN to work on a fresh machine until now! In the end I resorted to a manual install of the module.
I've also written this is the style of Perl that I used to write, although I believe/hope that there are now better methods of passing arguments and doing reverse loops.
The default print option is nice, however, and it has the best accuracy of all the standard (i.e. non-big int) libraries. Primarily because it uses Math::BigInt under the hood!
<?php // apt-get install php-pear // pear install Math_Fraction-0.4.1 include "Math/Fraction.php"; include "Math/FractionOp.php"; function calculateBern($bern) { $triangle = []; for($m=0;$m<=$bern;++$m) { $triangle[] = new Math_Fraction(1, $m+1); for($j=$m;$j>=1;--$j) { $triangle[$j-1] = Math_FractionOp::sub($triangle[$j-1], $triangle[$j], false); $triangle[$j-1] = Math_FractionOp::mult($triangle[$j-1], new Math_Fraction($j, 1), false); } } // There is an issue in Math_Fraction(267) which returns a ptr to a Math_Fraction and not // a reference. Therefore we manually simplify the fraction like this. $n = $triangle[0]->getNum(); $d = $triangle[0]->getDen(); $gcd = Math_FractionOp::gcd($n, $d); return new Math_Fraction($n/$gcd, $d/$gcd); } $bern = $argc > 1 ? intval($argv[1]) : 18; print 'All Bernouilli numbers up to ' . $bern . PHP_EOL; for($b=0;$b<=$bern;++$b) { print calculateBern($b)->toString() . PHP_EOL; } ?>
This was the first version I wrote which used an external library.
And it was the only time I found a show-stopping bug in a library!
My thoughts was of exasperation - why PHP! It has such a bad reputation that I daren't mention the issue for ages, lest I get accused of a witch hunt.
from fractions import Fraction from sys import argv def calculateBern(bern): values = [] for m in range(0, bern+1): values.append(Fraction(1, m+1)) for j in range(m, 0, -1): values[j-1] -= values[j] values[j-1] *= j return values[0] if (len(argv) < 2): bern = int(raw_input('Computer to which Bernouilli number? ')) else: bern = int(argv[1]) print 'All Bernouilli numbers up to', bern for b in range(1, bern+1): print calculateBern(b)
Although I have never really liked Python (Yes - it's due to the whitespace!) I have also liked the simplicity and elegance of this method. And the fact that the library worked (as opposed to the PHP version which preceded it) was a bonus.
Since Python is oft-used as a command line scripting language, I decided to remind myself of the syntax for bring the arguments into play.
# Requires: # gem install fractional require 'fractional' begin def calculateBernoulli(bern) row = [] for m in 0..bern row[m] = Fractional.new('1/' + (m+1).to_s) m.downto(1) { |j| row[j-1] -= row[j] row[j-1] *= j } end row[0] end for bern in 1..19 p calculateBernoulli(bern).to_s end end
Since Ruby was my 'day job' language, I wanted to include a few of my favourite parts of the language: ranges, downto, blocks, and last clause evaluated is returned. There's not enough scope to show all of Ruby's "good parts", alas, but I could at least show two different for loops.
It's a shame the Fractional gem doesn't have a better constructor.
Coding with _only_ globals is something I (now) find really difficult. ISTR I would use upper case for one, and lower case for the other, but I can't recall which way around. Thus, this version is a zombie of both as I used lower case for globals but, in retrospect, it should have been the other way around, but I was too lazy to change everything I'd just done. Additionally, I started my Sinclair career on the ZX81, where only upper case character were available. This might explain my excessive use of upper case variable names.
I remember using REM on the line before the method, too, so adopted that convention here. I also remember the layout for almost all of the Spectrum key maps, although it was made more difficult by ( and ) being on the wrong keys. There's also a routine in there to compute the modulus, since the Spectrum doesn't have one built in. This is a surprise to me now, but at the time I probably wouldn't have used it, it is' not something I'd forgotten - just something I never knew. I thought I use the Int(n/d) trick, but there's no Int method, either! (Whereas the - susposed inferior - ZX81 did!)
Keen eyed readers will also spot the spelling mistake in 'Calculatng'. I kept it in since I would probably have made the same mistake as a 12 year old (when I last wrote using Sinclair BASIC.)
It's also my first iterative approach to the GCD algorithm. Although, TBH, it's pretty much tail recursion so I could have taken this approach before.
Also, it's my first algorithm to use GOTO as an instruction.
I've used things, like sprintf, in places even though there are better mechanisms in place. My reason: I felt like it. Nostalgia. Boredom. Laziness. All of the above!
So many languages invent themselves to fix perceived issues within an existing language (like Coffeescript) whereas most of the functionality could have be achieved by the developer showing some (more?) discipline or understanding of the language. (I believe most devs hate C++ because they think it's too complex, whereas they haven't spent the time learning it.)
Good ideas get stolen (ranges, like 1..10). Sometimes without the necessary framework to effectively support it. Sometimes good ideas get stolen (such as 'use strict' from Perl, now in Javascript) without anyone knowing (or even acknowleding) from where they came.)
Enumeration is sometimes called 'comprehensions', it seems. Who knows why!?!? :)
No one can agreed on how scope should be implemented!
I changed my mind about names throughout...
I used libraries and extensions whenever I fancied a change. There's always a logic to which I choose, even if the logic is opaque. Roughly:
If/when I consider the language useful to me in command line applications, I'll parse the user's arguments. e.g. python. But most of the time, I won't.
When returning to old languages I'd not used for a few years I:
Sometimes I'll write a pretty printer for the result, eliminating the rendering of '0/0', for example. Sometimes, not. It depends on whether there's interesting language scructures that I could recall to do so.
I ended up settling on 17 terms, as most languages will show the precision issue by then if they have it. Almost non-big int versions will suffer at the 18th term. Forth I let run further because it as so painful to get going, but when it did showed some excellent results.
I never could decide my preference between 1+m or m+1. I changed between them according to aeshetics, algorithmic meaning, and boredom!
My naming for the loops, m and j, were kept fairly consistent... even though the names are very poorly chosen. As with 'real' development, early mistakes and legacy naming permeates everything.
I am still touring this talk to educational and technology conferences across the country. But, if means must, then you can always
watch the video here:

I had forgotten a lot about the language... but almost none of the keyboard shortcuts. I'm not sure what it says about me, exactly, but I'm sure everyone has their own ideas about that!
I kind of like the idea of meta-variables like PARAM and PARAM$ to hold the most recent return value, as it allows them to be easily optimized by the compiler - something that would have been important then, but less so now.
The use of [] for procedure arguments now seems alien, as they're more commonly used for arrays, but then it saved confusion between the two. I do like the nice symmetrical use of [] as syntax to pass arguments both into, and out of, the procedure.
I had issues with AMOS considering 0/0 as an error, rather than a result of 0. This code, which I ultimately submitted, does not have such issues.
There is a bug in this, as the numbers exceed the limits very quickly. But it's not important to me, ATM, to find it.